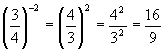Potencias:
Una potencia es un producto de factores iguales. Está formada por la base y el exponente.
| | Exponente |
Se puede leer:
tres elevado a cuatro o bien tres elevado a la cuarta
|
| 3 . 3 . 3 . 3 = 34 | |
| | Base |
El factor que se repite se llama base. El número de veces que se repite el factor, o sea la base, se llama exponente. Esto significa que si se tiene la potencia 2 6 (dos elevado a seis o a la sexta), la base será 2 y el exponente 6, lo cual dará como resultado 64 porque el 2 se multiplica por si mismo 6 veces (2 · 2 · 2 · 2 · 2 · 2 = 64).
Ejemplos:
2 5 = 2 • 2 • 2 • 2 • 2 = 32 El exponente es 5, esto significa que la base, el 2, se debe multiplicar por sí misma cinco veces.
3 2 = 3 • 3 = 9 El exponente es 2, esto significa que la base (3) se debe multiplicar por sí misma dos veces.
5 4 = 5 • 5 • 5 • 5 = 625 El exponente es 4, esto significa que la base (5) se debe multiplicar por sí misma cuatro veces.
Una potencia puede representarse en forma general como:
| an = a • a • a • ........ |
Donde: a = base n = exponente “ n” factores iguales
Finalmente, recuerda que una de las aplicaciones de las potencias es la descomposición factorial de un número.
Potencia de base entera y exponente natural
Si la base
a pertenece al conjunto de los
Números Enteros ( a 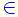 Z )
Z ) (léase
a pertenece a zeta) significa que puede tomar valores
positivos y
negativos. Si el exponente pertenece al conjunto de los
Números Naturales, significa que puede tomar valores del uno en adelante (1, 2, 3, .....).
Potencia de base entera positiva:
Si la base a es positiva, la potencia siempre será un entero positivo, independiente de los valores que tome el exponente, es decir, de que sea par o impar.
Ejemplos:
(+4) 3 = 43 = 4 • 4 • 4 = 64 = + 64 Exponente impar
(+3) 4 = 34 = 3 • 3 • 3 • 3 = 81 = +81 Exponente par
Potencia de base entera negativa:
Si la base a es negativa el signo de la potencia dependerá de si el exponente es par o impar.
a) Si el exponente es par, la potencia es positiva.
Ejemplos:
(_5) 2 = _5 • _5 = +25 = 25 _ · _ = +
(_2) 8 = _2 • _2 • _2 • _2 • _2 • _2 • _2 • _2 = +256 = 256
b) Si el exponente es impar, la potencia es negativa.
Ejemplos:
(_2) 3 = _2 • _2 • _2 = _8
(_3) 3 = _3 • _3 • _3 = _27
En resumen:
Base
|
Exponente
|
Potencia
|
Positiva
|
Par
|
Positiva
|
Positiva
|
Impar
|
Positiva
|
Negativa
|
Par
|
Positiva
|
Negativa
|
Impar
|
Negativa
|
Multiplicación de potencias de igual base
Para multiplicar potencias de igual base, se suman los exponentes y se mantiene la base.
Ejemplos:
1)
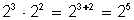
2)
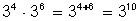
3)
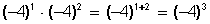
División de potencias de igual base
Para dividir potencias de igual base, se restan los exponentes y se conserva la base.
Ejemplos:
1)
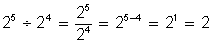
2)
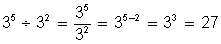
3)
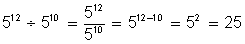
Multiplicación de potencias de igual exponente
Se multiplican las bases y se conserva el exponente.
Ejemplo:
División de potencias de igual exponente
Se dividen las bases y se conserva el exponente
Ejemplo:
Potencia elevada a potencia
Se eleva la base al producto (multiplicación) de los exponentes; o sea, se conserva la base y se multiplican los exponentes.
Ejemplos:
1)
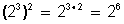
2)
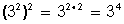
Potencia de base racional y exponente entero
Sea la base
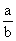
(fracción) perteneciente al conjunto de los Números Racionales (
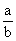
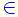
Q ), donde
a es el numerador y
b el denominador distinto de cero, y el exponente pertenece a los números enteros (n
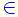
Z). Para elevar una fracción a potencia se elevan por separado numerador y denominador.
Ejemplos:
1)
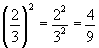
2)
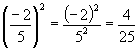
3)
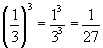
Potencia de exponente negativo
Si
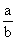
es un número racional y – n un número entero, entonces se tiene,
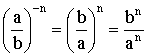 | Si el exponente es negativo el numerador se invierte con el denominador, y el exponente cambia de signo. |
Ejemplos:
1)
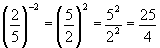
2)
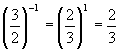
3)